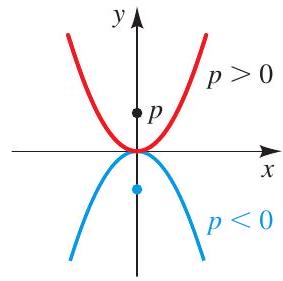
A parabola is the set of points in the plane that are equidistant from a fixed point \(F\) (the focus) and a fixed line \(l\) (the directrix).
A parabola with vertex at the origin has one of the following standard equations.

Focus \((0, p)\), directrix \(y=-p\)
\(y^{2}=4 p x\)
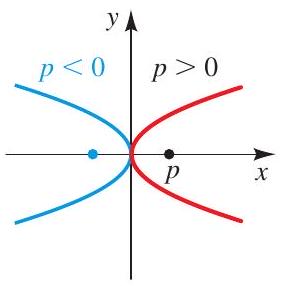
Focus \((p, 0)\), directrix \(x=-p\)
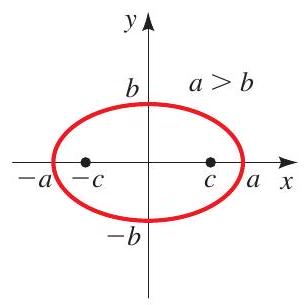
An ellipse is the set of all points in the plane for which the sum of the distances to each of two given points \(F_{1}\) and \(F_{2}\) (the foci) is a fixed constant.
An ellipse with center at the origin has one of the following standard equations.
Foci \(( \pm c, 0), c^{2}=a^{2}-b^{2}\)
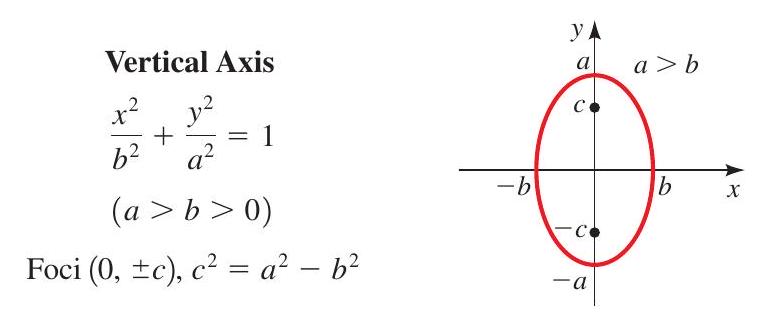
The eccentricity of an ellipse with equation \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) or \(\frac{x^{2}}{b^{2}}+\frac{y^{2}}{a^{2}}=1(\) where \(a>b>0)\) is the number
where \(c=\sqrt{a^{2}-b^{2}}\). The eccentricity \(e\) of any ellipse is a number between 0 and 1 . If \(e\) is close to 0 , then the ellipse is nearly circular; the closer \(e\) gets to 1 , the more elongated the ellipse becomes.
A hyperbola is the set of all points in the plane for which the absolute value of the difference of the distances to each of two given points \(F_{1}\) and \(F_{2}\) (the foci) is a fixed constant.
A hyperbola with center at the origin has one of the following standard equations.
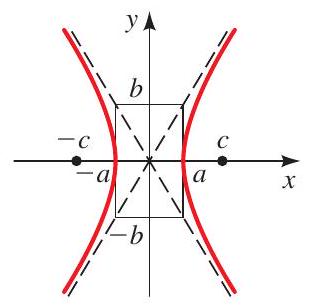
Foci \(( \pm c, 0), c^{2}=a^{2}+b^{2}\)
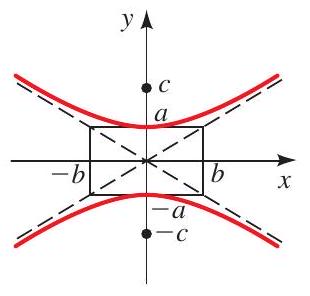 \(\operatorname{Foci}(0, \pm c), c^{2}=a^{2}+b^{2}\)
\(\operatorname{Foci}(0, \pm c), c^{2}=a^{2}+b^{2}\)
If the vertex of a parabola or the center of an ellipse or a hyperbola does not lie at the origin but rather at the point \((h, k)\), then we refer to the curve as a shifted conic. To find the equation of the shifted conic, we use the "unshifted" form for the appropriate curve and replace \(x\) by \(x-h\) and \(y\) by \(y-k\).
The graph of the equation
(where \(A\) and \(C\) are not both 0 ) is either a conic or a degenerate conic. In the nondegenerate cases the graph is
To graph a conic whose equation is given in general form, complete the squares in \(x\) and \(y\) to put the equation in standard form for a parabola, an ellipse, or a hyperbola.
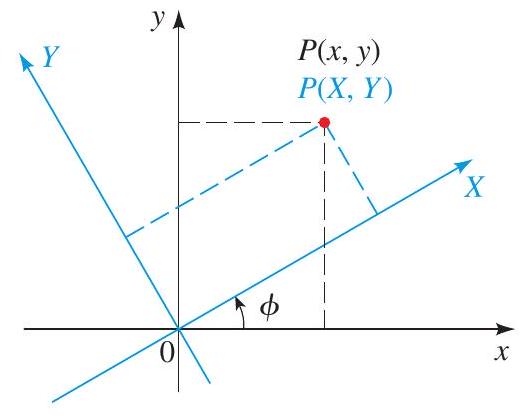
Suppose the \(x\) - and \(y\)-axes in a coordinate plane are rotated through the acute angle \(\phi\) to produce the \(X\) - and \(Y\)-axes, as shown in the figure. Then the coordinates of a point in the \(x y\) - and the \(X Y\)-planes are related as follows:
The general equation of a conic is of the form
The quantity \(B^{2}-4 A C\) is called the discriminant of the equation. The graph is
To eliminate the \(x y\)-term in the general equation of a conic, rotate the axes through an angle \(\phi\) that satisfies
A polar equation of the form
represents a conic with one focus at the origin and with eccentricity \(e\). The conic is