chapter5_review.md

The Unit Circle

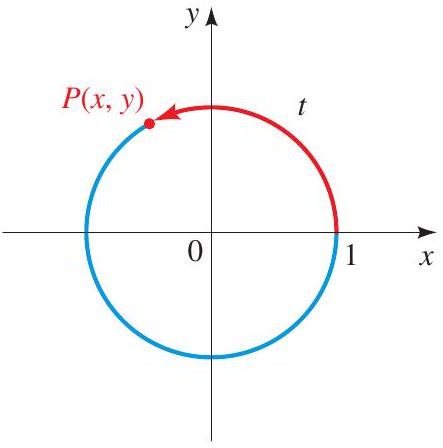
The unit circle is the circle of radius 1 centered at $(0, 0)$ . The equation of the unit circle is $x^{2} + y^{2} = 1$ .

Terminal Points on the Unit Circle

The terminal point $P (x, y)$ determined by the real number $t$ is the point obtained by traveling counterclockwise a distance $t$ along the unit circle, starting at $(1, 0)$ .

Special terminal points are listed in Table 5.1.1.

The Reference Number

The reference number associated with the real number $t$ is the shortest distance along the unit circle between the terminal point determined by $t$ and the $x$ -axis.

The Trigonometric Functions

Let $P (x, y)$ be the terminal point on the unit circle determined by the real number $t$ . Then for nonzero values of the denominator the trigonometric functions are defined as follows.

\begin{array}{lll} \sin t = y & \cos t = x & \tan t = \frac{y}{x} \\ \csc t = \frac{1}{y} & \sec t = \frac{1}{x} & \cot t = \frac{x}{y} \end{array}

Special Values of the Trigonometric Functions

The trigonometric functions have the following values at the special values of $t$ .

$t$	$s i n t$	$c o s t$	$t a n t$	$c s c t$	$\sec t$	$c o t t$
0	0	1	0	-	1	-
$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{3}}{3}$	2	$\frac{2 \sqrt{3}}{3}$	$\sqrt{3}$
$\frac{π}{4}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{2}}{2}$	1	$\sqrt{2}$	$\sqrt{2}$	1
$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$	$\frac{2 \sqrt{3}}{3}$	2	$\frac{\sqrt{3}}{3}$
$\frac{π}{2}$	1	0	-	1	-	0
$π$	0	-1	0	-	-1	-
$\frac{3 π}{2}$	-1	0	-	-1	-	0

Basic Trigonometric Identities

An identity is an equation that is true for all values of the variable. The basic trigonometric identities are as follows.

Reciprocal Identities

\csc t = \frac{1}{\sin t} \sec t = \frac{1}{\cos t} \cot t = \frac{1}{\tan t}

Pythagorean Identities

\begin{aligned} \sin^{2} t + \cos^{2} t & = 1 \\ \tan^{2} t + 1 & = \sec^{2} t \\ 1 + \cot^{2} t & = \csc^{2} t \end{aligned}

Even-Odd Properties

\begin{array}{lll} \sin (- t) = - \sin t & \cos (- t) = \cos t & \tan (- t) = - \tan t \\ \csc (- t) = - \csc t & \sec (- t) = \sec t & \cot (- t) = - \cot t \end{array}

Periodic Properties

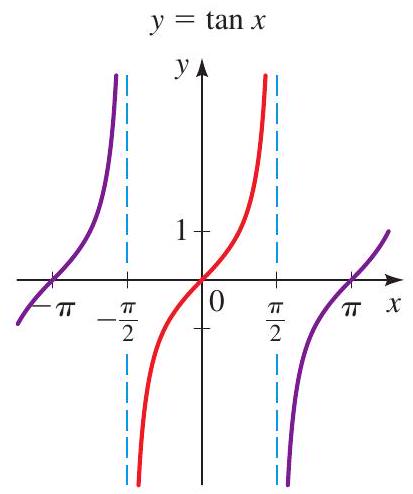
A function $f$ is periodic if there is a positive number $p$ such that $f (x + p) = f (x)$ for every $x$ . The least such $p$ is called the period of $f$ . The sine and cosine functions have period $2 π$ , and the tangent function has period $π$ .

\begin{aligned} \sin (t + 2 π) & = \sin t \\ \cos (t + 2 π) & = \cos t \\ \tan (t + π) & = \tan t \end{aligned}

Graphs of the Sine and Cosine Functions

The graphs of sine and cosine have amplitude 1 and period $2 π$ .

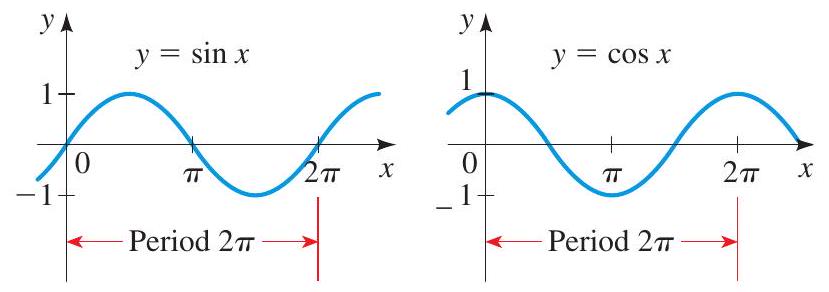
Amplitude 1, Period $2 π$

Graphs of Transformations of Sine and Cosine | Section 5.3

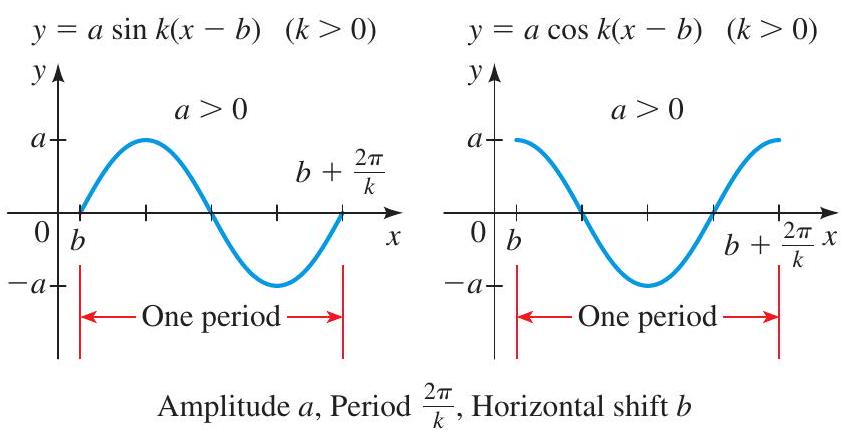
An appropriate interval on which to graph one complete period is $[b, b + (2 π / k)]$ .

Graphs of the Tangent and Cotangent Functions

These functions have period $π$ .

$y = \cot x$

To graph one period of $y = a \tan k x$ , an appropriate interval is $(- \frac{π}{2 k}, \frac{π}{2 k})$ . To graph one period of $y = a \cot k x$ , an appropriate interval is $(0, \frac{π}{k})$ .

Graphs of the Secant and Cosecant Functions

These functions have period $2 π$ .

y = \sec x

To graph one period of $y = a \sec k x$ or $y = a \csc k x$ , an appropriate interval is $(0, \frac{2 π}{k})$ .

Inverse Trigonometric Functions

Inverse functions of the trigonometric functions have the following domain and range.

Function	Domain	Range
$\sin^{- 1}$	$[- 1, 1]$	$[- \frac{π}{2}, \frac{π}{2}]$
$\cos^{- 1}$	$[- 1, 1]$	$[0, π]$
$\tan^{- 1}$	$(- \infty, \infty)$	$(- \frac{π}{2}, \frac{π}{2})$

The inverse trigonometric functions are defined as follows.

\begin{aligned} \sin^{- 1} x = y & \Leftrightarrow \sin y = x \\ \cos^{- 1} x = y & \Leftrightarrow \cos y = x \\ \tan^{- 1} x = y & \Leftrightarrow \tan y = x \end{aligned}

Graphs of these inverse functions are shown below.

Harmonic Motion

An object is in simple harmonic motion if its displacement $y$ at time $t$ is modeled by $y = a \sin ω t$ or $y = a \cos ω t$ . In this case the amplitude is $| a |$ , the period is $2 π / ω$ , and the frequency is $ω / (2 π)$ .

Damped Harmonic Motion

An object is in damped harmonic motion if its displacement $y$ at time $t$ is modeled by $y = k e^{- c t} \sin ω t$ or $y = k e^{- c t} \cos ω t, c > 0$ . In this case $c$ is the damping constant, $k$ is the initial amplitude, and $2 π / ω$ is the period.

Phase

Any sine curve can be expressed in the following equivalent forms:

\begin{array}{ll} y = A \sin (k t - b), & the phase is b \\ y = A \sin k (t - \frac{b}{k}), & the horizontal shift is \frac{b}{k} \end{array}

The phase (or phase angle) $b$ is the initial angular position of the motion. The number $b / k$ is also called the lag time $(b > 0)$ or lead time $(b < 0)$ .

Suppose that two objects are in harmonic motion with the same period modeled by

y_{1} = A \sin (k t - b) and y_{2} = A \sin (k t - c)

The phase difference between $y_{1}$ and $y_{2}$ is $b - c$ . The motions are "in phase" if the phase difference is a multiple of $2 π$ ; otherwise, the motions are "out of phase."