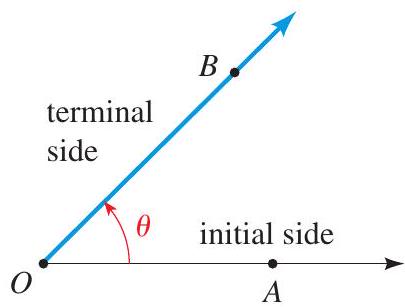
An angle consists of two rays with a common vertex. One of the rays is the initial side, and the other the terminal side. An angle can be viewed as a rotation of the initial side onto the terminal side. If the rotation is counterclockwise, the angle is positive; if the rotation is clockwise, the angle is negative.

Notation: The angle in the figure can be referred to as angle \(A O B\), or simply as angle \(O\), or as angle \(\theta\).
The radian measure of an angle (abbreviated rad) is the length of the arc that the angle subtends in a circle of radius 1 , as shown in the figure.
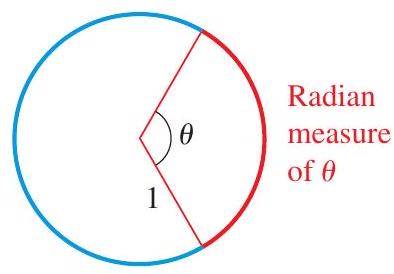
The degree measure of an angle is the number of degrees in the angle, where a degree is \(\frac{1}{360}\) of a complete circle.
To convert degrees to radians, multiply by \(\pi / 180\). To convert radians to degrees, multiply by \(180 / \pi\).
An angle is in standard position if it is drawn in the \(x y\)-plane with its vertex at the origin and its initial side on the positive \(x\)-axis.
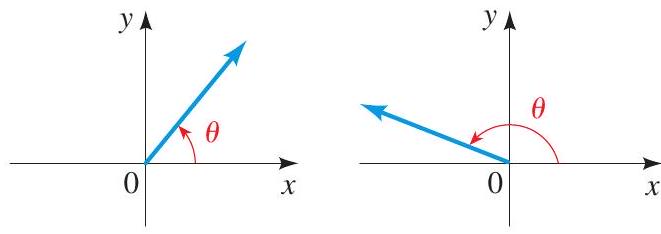
Two angles in standard position are coterminal if their terminal sides coincide. The reference angle \(\bar{\theta}\) associated with an angle \(\theta\) is the acute angle formed by the terminal side of \(\theta\) and the \(x\)-axis.
Consider a circle of radius \(r\).
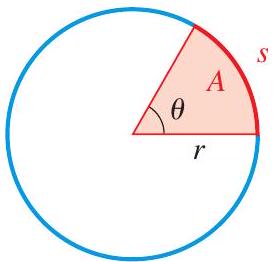
The length \(s\) of an arc that subtends a central angle of \(\theta\) radians is \(s=r \theta\).
The area \(A\) of a sector with central angle of \(\theta\) radians is \(A=\frac{1}{2} r^{2} \theta\).
Suppose a point moves along a circle of radius \(r\) and the ray from the center of the circle to the point traverses \(\theta\) radians in time \(t\). Let \(s=r \theta\) be the distance the point travels in time \(t\).
The angular speed of the point is \(\omega=\theta / t\). The linear speed of the point is \(v=s / t\). Linear speed \(v\) and angular speed \(\omega\) are related by the formula \(v=r \omega\).
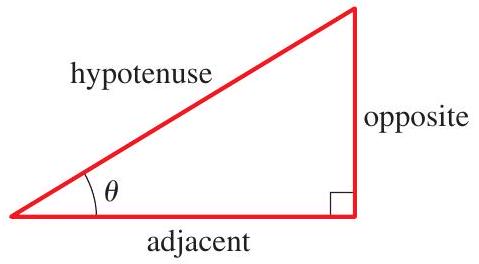
For a right triangle with an acute angle \(\theta\) the trigonometric ratios are defined as follows.
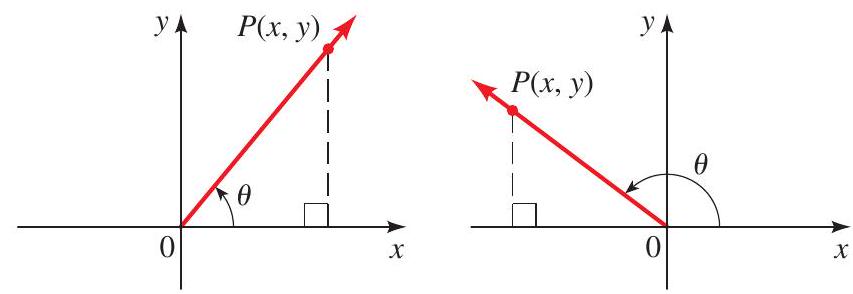
Let \(\theta\) be an angle in standard position, and let \(P(x, y)\) be a point on the terminal side, as shown in the figures. Let \(r=\sqrt{x^{2}+y^{2}}\) be the distance from the origin to the point \(P(x, y)\).
For nonzero values of the denominator the trigonometric functions are defined as follows.
The following table gives the values of the trigonometric functions at some special angles.
| \(\boldsymbol{\theta}\) | \(\boldsymbol{\theta}\) | \(\boldsymbol{\operatorname { s i n } \boldsymbol { \theta }}\) | \(\boldsymbol{\operatorname { c o s } \theta}\) | \(\boldsymbol{\operatorname { t a n }} \boldsymbol{\theta}\) | \(\boldsymbol{\operatorname { c s c } \theta}\) | \(\boldsymbol{\operatorname { s e c } \theta}\) | \(\boldsymbol{\operatorname { c o t } \theta \boldsymbol { \theta }}\) |
|---|---|---|---|---|---|---|---|
| \(0^{\circ}\) | 0 | 0 | 1 | 0 | - | 1 | - |
| \(30^{\circ}\) | \(\frac{\pi}{6}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{\sqrt{3}}{3}\) | 2 | \(\frac{2 \sqrt{3}}{3}\) | \(\sqrt{3}\) |
| \(45^{\circ}\) | \(\frac{\pi}{4}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 | \(\sqrt{2}\) | \(\sqrt{2}\) | 1 |
| \(60^{\circ}\) | \(\frac{\pi}{3}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\sqrt{3}\) | \(\frac{2 \sqrt{3}}{3}\) | 2 | \(\frac{\sqrt{3}}{3}\) |
| \(90^{\circ}\) | \(\frac{\pi}{2}\) | 1 | 0 | - | 1 | - | 0 |
| \(180^{\circ}\) | \(\pi\) | 0 | -1 | 0 | - | -1 | - |
| \(270^{\circ}\) | \(\frac{3 \pi}{2}\) | -1 | 0 | - | -1 | - | 0 |
An identity is an equation that is true for all values of the variable. The basic trigonometric identities follow.
Pythagorean Identities:
The area \(\mathscr{A}\) of a triangle with sides of lengths \(a\) and \(b\) and with included angle \(\theta\) is
Inverse functions of the trigonometric functions have the domain and range shown in the following table.
| Function | Domain | Range |
|---|---|---|
| \(\sin ^{-1}\) | \([-1,1]\) | \(\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]\) |
| \(\cos ^{-1}\) | \([-1,1]\) | \([0, \pi]\) |
| \(\tan ^{-1}\) | \((-\infty, \infty)\) | \(\left(-\frac{\pi}{2}, \frac{\pi}{2}\right)\) |
The inverse trigonometric functions are defined as follows.
We follow the convention of labeling the angles of a triangle as \(A, B, C\) and the lengths of the corresponding opposite sides as \(a, b, c\), as labeled in the figure.
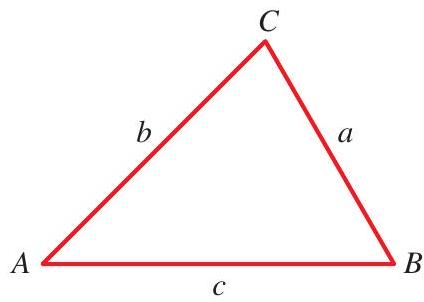
For a triangle \(A B C\) we have the following laws. The Law of Sines states that
The Law of Cosines states that
Let \(A B C\) be a triangle with sides \(a, b\), and \(c\).
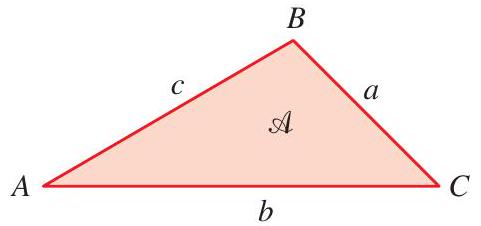
Heron's Formula states that the area \(\mathscr{A}\) of triangle \(A B C\) is
where \(s=\frac{1}{2}(a+b+c)\) is the semiperimeter of the triangle.