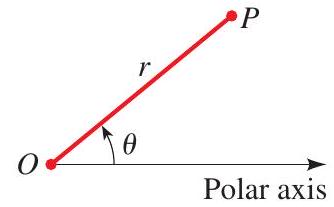
In the polar coordinate system the location of a point \(P\) in the plane is determined by an ordered pair \((r, \theta)\), where \(r\) is the distance from the pole \(O\) to \(P\) and \(\theta\) is the angle formed by the polar axis and the segment \(\overrightarrow{O P}\), as shown in the figure.

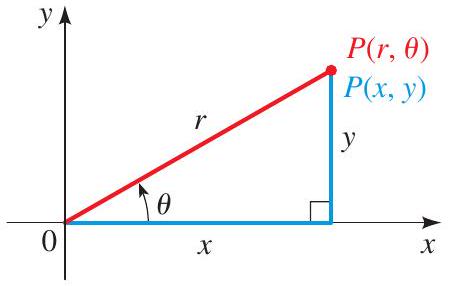
Any point \(P\) in the plane has polar coordinates \(P(r, \theta)\) and rectangular coordinates \(P(x, y)\), as shown.
A polar equation is an equation in the variables \(r\) and \(\theta\). The graph of a polar equation \(r=f(\theta)\) consists of all points \((r, \theta)\) whose coordinates satisfy the equation.
The graph of a polar equation is
A complex number is a number of the form \(a+b i\), where \(i^{2}=-1\) and where \(a\) and \(b\) are real numbers. For the complex number \(z=a+b i, a\) is called the real part and \(b\) is called the imaginary part. A complex number \(a+b i\) is graphed in the complex plane as shown.
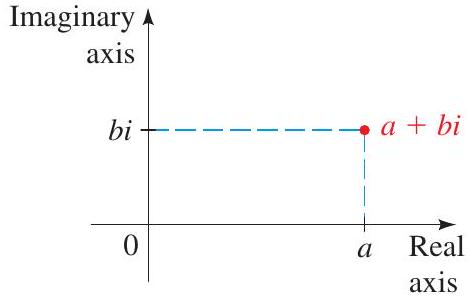
The modulus (or absolute value) of a complex number \(z=a+b i\) is
A complex number \(z=a+b i\) has the polar form (or trigonometric form)
where \(r=|z|\) and \(\tan \theta=b / a\). The number \(r\) is the modulus of \(z\) and \(\theta\) is the argument of \(z\).
Suppose the complex numbers \(z_{1}\) and \(z_{2}\) have the following polar form:
Then
If \(z=r(\cos \theta+i \sin \theta)\) is a complex number in polar form and \(n\) is a positive integer, then
If \(z=r(\cos \theta+i \sin \theta)\) is a complex number in polar form and \(n\) is a positive integer, then \(z\) has the \(n\) distinct \(n\)th roots \(w_{0}, w_{1}, \ldots, w_{n-1}\), where
where \(k=0,1,2, \ldots, n-1\).
To find the \(n\)th roots of \(z=r(\cos \theta+i \sin \theta)\), we use the following observations:
If \(f\) and \(g\) are functions defined on an interval \(I\), then the set of points \((f(t), g(t))\) is a plane curve. The equations
where \(t \in I\), are parametric equations for the curve, with parameter \(t\).
The graph of the polar equation \(r=f(\theta)\) is the same as the graph of the parametric equations
A vector is a quantity with both magnitude and direction. A vector in the coordinate plane is expressed in terms of two coordinates or components
If a vector \(\mathbf{v}\) has its initial point at \(P\left(x_{1}, y_{1}\right)\) and its terminal point at \(Q\left(x_{2}, y_{2}\right)\), then
Let \(\mathbf{u}=\left\langle a_{1}, a_{2}\right\rangle, \mathbf{v}=\left\langle b_{1}, b_{2}\right\rangle\), and \(c \in \mathbb{R}\). The operations on vectors are defined as follows.
The unit vectors \(\mathbf{i}\) and \(\mathbf{j}\) are defined by
Any vector \(\mathbf{v}=\left\langle a_{1}, a_{2}\right\rangle\) can be expressed as